Welcome to another journey into the world of algorithms! Today, we’re unraveling the mysteries of the Selection Sort algorithm, a simple yet powerful sorting technique. What makes this exploration unique is that we’ll be dissecting each step of the process, shedding light on the intricacies that make Selection Sort tick. Let’s dive in!
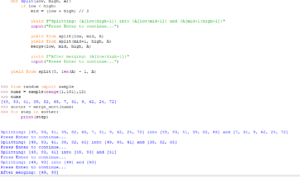
>>> def selection_sort(A:list):
min = None
print("Start list: ", A)
for i in range(len(A)-1):
min = i
print(A[:i], A[i:])
print(f'Initial minimum set to: {A[min]}')
for j in range(i+1, len(A)):
if A[j] < A[min]:
min = j
if min != i:
print(f'Updated minimum: {A[min]}')
A[i],A[min] = A[min],A[i]
print(A[:i+1], A[i+1:])
yield i
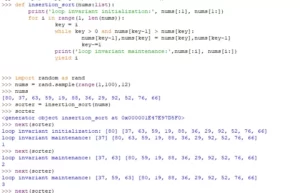
>>> from random import sample
>>> nums = sample(range(1,101),12)
>>> nums
[12, 38, 35, 24, 60, 30, 69, 75, 54, 88, 45, 98]
>>> sorter = selection_sort(nums)
>>> next(sorter)
Start list: [12, 38, 35, 24, 60, 30, 69, 75, 54, 88, 45, 98]
[] [12, 38, 35, 24, 60, 30, 69, 75, 54, 88, 45, 98]
Initial minimum set to: 12
[12] [38, 35, 24, 60, 30, 69, 75, 54, 88, 45, 98]
0
>>> next(sorter)
[12] [38, 35, 24, 60, 30, 69, 75, 54, 88, 45, 98]
Initial minimum set to: 38
Updated minimum: 24
[12, 24] [35, 38, 60, 30, 69, 75, 54, 88, 45, 98]
1
>>> next(sorter)
[12, 24] [35, 38, 60, 30, 69, 75, 54, 88, 45, 98]
Initial minimum set to: 35
Updated minimum: 30
[12, 24, 30] [38, 60, 35, 69, 75, 54, 88, 45, 98]
2
>>> next(sorter)
[12, 24, 30] [38, 60, 35, 69, 75, 54, 88, 45, 98]
Initial minimum set to: 38
Updated minimum: 35
[12, 24, 30, 35] [60, 38, 69, 75, 54, 88, 45, 98]
3
>>> next(sorter)
[12, 24, 30, 35] [60, 38, 69, 75, 54, 88, 45, 98]
Initial minimum set to: 60
Updated minimum: 38
[12, 24, 30, 35, 38] [60, 69, 75, 54, 88, 45, 98]
4
>>> next(sorter)
[12, 24, 30, 35, 38] [60, 69, 75, 54, 88, 45, 98]
Initial minimum set to: 60
Updated minimum: 45
[12, 24, 30, 35, 38, 45] [69, 75, 54, 88, 60, 98]
5
>>> next(sorter)
[12, 24, 30, 35, 38, 45] [69, 75, 54, 88, 60, 98]
Initial minimum set to: 69
Updated minimum: 54
[12, 24, 30, 35, 38, 45, 54] [75, 69, 88, 60, 98]
6
>>> next(sorter)
[12, 24, 30, 35, 38, 45, 54] [75, 69, 88, 60, 98]
Initial minimum set to: 75
Updated minimum: 60
[12, 24, 30, 35, 38, 45, 54, 60] [69, 88, 75, 98]
7
>>> next(sorter)
[12, 24, 30, 35, 38, 45, 54, 60] [69, 88, 75, 98]
Initial minimum set to: 69
[12, 24, 30, 35, 38, 45, 54, 60, 69] [88, 75, 98]
8
>>> next(sorter)
[12, 24, 30, 35, 38, 45, 54, 60, 69] [88, 75, 98]
Initial minimum set to: 88
Updated minimum: 75
[12, 24, 30, 35, 38, 45, 54, 60, 69, 75] [88, 98]
9
>>> next(sorter)
[12, 24, 30, 35, 38, 45, 54, 60, 69, 75] [88, 98]
Initial minimum set to: 88
[12, 24, 30, 35, 38, 45, 54, 60, 69, 75, 88] [98]
10
>>> next(sorter)
Traceback (most recent call last):
File "<pyshell#17>", line 1, in <module>
next(sorter)
StopIteration
>>> nums
[12, 24, 30, 35, 38, 45, 54, 60, 69, 75, 88, 98]
>>> Understanding the Output:
In the output provided, you can observe the list being sorted step by step. Each line of the output is a snapshot of the algorithm’s progress, showcasing the state of the list at a particular point in time.
- Left Display: Represents the sorted portion of the list after each iteration.
- Right Display: Shows the unsorted portion of the list after each iteration.
- Initial Minimum: The starting point for finding the minimum value in the unsorted portion.
- Updated Minimum: The new minimum value discovered during the iteration.
- Swap Operation: Executed when the updated minimum is different from the initial minimum, ensuring the list remains in ascending order.
Unraveling the Iterations:
The real magic happens as we progress through each iteration, witnessing the interplay between the left and right displays. Let’s break down the second iteration:
- Iteration Continues: The process unfolds, and the left and right displays evolve accordingly.
- Initial Minimum: Reset to the first element of the unsorted portion (60).
- Updated Minimum: Now identified as 45.
- Swap Operation: Another swap takes place, maintaining the ascending order of the list.
Significance of Displays and Minimum Values:
The left and right displays serve as a visual aid, allowing us to witness the list’s transformation at each stage. Meanwhile, the initial and updated minimum values play a crucial role in determining when to perform a swap. This decision-making process ensures that the smallest unsorted element finds its rightful place in the sorted portion of the list.
Conclusion:
By peeling back the layers of Selection Sort and understanding the output’s nuances, we gain valuable insights into how the algorithm systematically organizes elements. The left and right displays provide a clear picture of the algorithm’s progress, while the initial and updated minimum values guide its decision-making. Armed with this knowledge, you’re better equipped to appreciate the elegance of Selection Sort.