The Divide and Conquer Paradigm
Merge Sort is more than just a sorting algorithm; it’s a testament to the power of the ‘divide and conquer’ paradigm. The algorithm strategically breaks down a complex sorting problem into smaller, more manageable subproblems. As we’ve seen in the video, this approach sets the stage for a more straightforward and faster sorting process.
>>> def merge_sort(A):
def merge(low, mid, high, A):
left, right = A[low:mid+1], A[mid+1:high+1]
i, j, k = 0, 0, low
while i < len(left) and j < len(right):
if left[i] < right[j]:
A[k] = left[i]
i += 1
else:
A[k] = right[j]
j += 1
k += 1
while i < len(left):
A[k] = left[i]
i += 1
k += 1
while j < len(right):
A[k] = right[j]
j += 1
k += 1
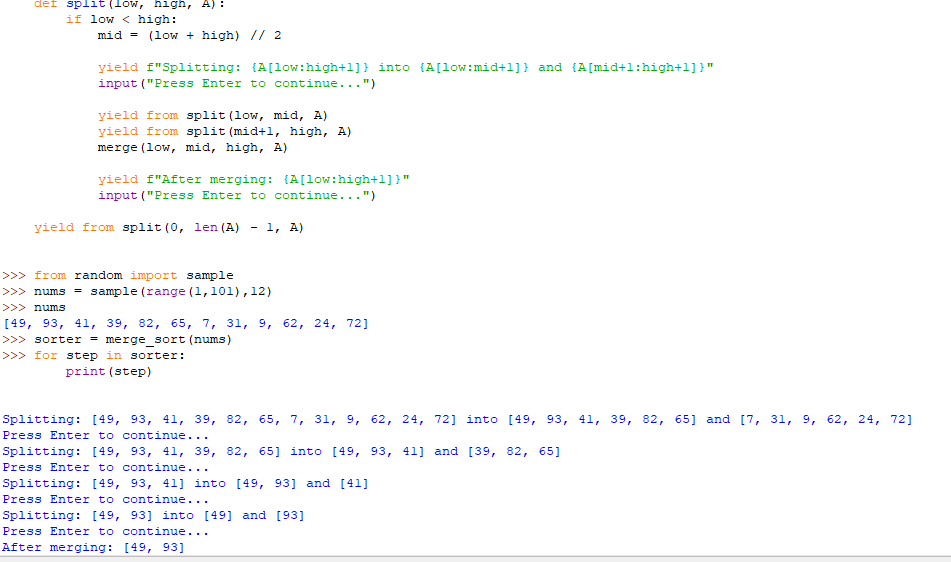
def split(low, high, A):
if low < high:
mid = (low + high) // 2
yield f"Splitting: {A[low:high+1]} into {A[low:mid+1]} and {A[mid+1:high+1]}"
input("Press Enter to continue...")
yield from split(low, mid, A)
yield from split(mid+1, high, A)
merge(low, mid, high, A)
yield f"After merging: {A[low:high+1]}"
input("Press Enter to continue...")
yield from split(0, len(A) - 1, A)
>>> from random import sample
>>> nums = sample(range(1,101),12)
>>> nums
[49, 93, 41, 39, 82, 65, 7, 31, 9, 62, 24, 72]
>>> sorter = merge_sort(nums)
>>> for step in sorter:
print(step)
Splitting: [49, 93, 41, 39, 82, 65, 7, 31, 9, 62, 24, 72] into [49, 93, 41, 39, 82, 65] and [7, 31, 9, 62, 24, 72]
Press Enter to continue...
Splitting: [49, 93, 41, 39, 82, 65] into [49, 93, 41] and [39, 82, 65]
Press Enter to continue...
Splitting: [49, 93, 41] into [49, 93] and [41]
Press Enter to continue...
Splitting: [49, 93] into [49] and [93]
Press Enter to continue...
After merging: [49, 93]
Press Enter to continue...
After merging: [41, 49, 93]
Press Enter to continue...
Splitting: [39, 82, 65] into [39, 82] and [65]
Press Enter to continue...
Splitting: [39, 82] into [39] and [82]
Press Enter to continue...
After merging: [39, 82]
Press Enter to continue...
After merging: [39, 65, 82]
Press Enter to continue...
After merging: [39, 41, 49, 65, 82, 93]
Press Enter to continue...
Splitting: [7, 31, 9, 62, 24, 72] into [7, 31, 9] and [62, 24, 72]
Press Enter to continue...
Splitting: [7, 31, 9] into [7, 31] and [9]
Press Enter to continue...
Splitting: [7, 31] into [7] and [31]
Press Enter to continue...
After merging: [7, 31]
Press Enter to continue...
After merging: [7, 9, 31]
Press Enter to continue...
Splitting: [62, 24, 72] into [62, 24] and [72]
Press Enter to continue...
Splitting: [62, 24] into [62] and [24]
Press Enter to continue...
After merging: [24, 62]
Press Enter to continue...
After merging: [24, 62, 72]
Press Enter to continue...
After merging: [7, 9, 24, 31, 62, 72]
Press Enter to continue...
After merging: [7, 9, 24, 31, 39, 41, 49, 62, 65, 72, 82, 93]
Press Enter to continue...
>>> nums
[7, 9, 24, 31, 39, 41, 49, 62, 65, 72, 82, 93]
>>> The Splitting Dance
At the core of Merge Sort is the art of splitting. In the video, we visualized how the algorithm intelligently divides our list into smaller, sorted subarrays. The ‘Splitting’ print statements showcased the elegance of breaking down a large problem into smaller, solvable subproblems. This step-by-step breakdown not only eases the sorting process but also lays the foundation for the subsequent merging.
The Crucial Merge Operation
While splitting divides the problem, the magic of Merge Sort happens during the merging phase. The ‘Merge’ function intelligently combines the sorted subarrays, restoring the original order. The efficiency of Merge Sort lies in its ability to merge these subarrays in a way that produces a fully sorted list.
Bringing It All Together
As we’ve witnessed in the video, the synergy of splitting and merging is what makes Merge Sort shine. Its O(n log n) time complexity positions it as a go-to algorithm for sorting tasks where efficiency is key.
Watch the Journey Unfold
If you haven’t already, check out our accompanying YouTube video where we step through the code, visualize the algorithm’s operation, and appreciate the elegance of Merge Sort.
Closing Thoughts
Merge Sort is not just an algorithm; it’s a journey into problem-solving strategies and algorithmic beauty. We hope this exploration has shed light on the inner workings of Merge Sort and inspired you in your coding endeavors.
Feel free to drop your comments on the video or this blog post. We’re always eager to hear your thoughts and engage in discussions about the fascinating world of algorithms.