Greetings, coding enthusiasts! Today, we embark on a fascinating journey into the world of sorting algorithms, and our spotlight is on the magical Insertion Sort. But hold on to your wizard hats because we’re not just delving into the theory — we’re visualizing the enchanting process using Python code.
The Deck of Cards Analogy
Now, the heart of our code is an implementation of Insertion Sort using Python, and we’ve added a special touch with the ‘yield’ keyword. Think about sorting numbers like sorting a deck of cards. We call these numbers ‘keys.’ Imagine you have a bunch of cards on the table, face down. Now, the cool part about insertion sort is it works just like sorting cards in your hand.
Picture this: you start with an empty hand on the left, and you grab one card at a time from the table. But, instead of just throwing them in randomly, you slide each card into its proper spot in your hand.
How do you know where it goes? Well, you compare it with the cards already in your hand, moving from right to left. So, it’s like you’re finding the perfect spot for each card in your hand.
Here’s the trick: your hand is always sorted. From the get-go, those cards in your hand were originally the top cards from the messy pile on the table. It’s like a neat and organized game of cards, but with numbers. That’s how insertion sort does its thing!
Python 3.9.0 (tags/v3.9.0:9cf6752, Oct 5 2020, 15:34:40) [MSC v.1927 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license()" for more information.
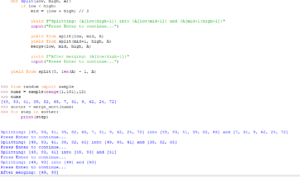
>>> def insertion_sort(nums:list):
print('loop invariant initialization:', nums[:1], nums[1:])
for i in range(1, len(nums)):
key = i
while key > 0 and nums[key-1] > nums[key]:
nums[key-1],nums[key] = nums[key],nums[key-1]
key-=1
print('loop invariant maintenance:',nums[:i], nums[i:])
yield i
>>> import random as rand
>>> nums = rand.sample(range(1,100),12)
>>> nums
[80, 37, 63, 59, 19, 88, 36, 29, 92, 52, 76, 66]
>>> sorter = insertion_sort(nums)
>>> sorter
<generator object insertion_sort at 0x000001E47E97D5F0>
>>> next(sorter)
loop invariant initialization: [80] [37, 63, 59, 19, 88, 36, 29, 92, 52, 76, 66]
loop invariant maintenance: [37] [80, 63, 59, 19, 88, 36, 29, 92, 52, 76, 66]
1
>>> next(sorter)
loop invariant maintenance: [37, 63] [80, 59, 19, 88, 36, 29, 92, 52, 76, 66]
2
>>> next(sorter)
loop invariant maintenance: [37, 59, 63] [80, 19, 88, 36, 29, 92, 52, 76, 66]
3
>>> next(sorter)
loop invariant maintenance: [19, 37, 59, 63] [80, 88, 36, 29, 92, 52, 76, 66]
4
>>> next(sorter)
loop invariant maintenance: [19, 37, 59, 63, 80] [88, 36, 29, 92, 52, 76, 66]
5
>>> next(sorter)
loop invariant maintenance: [19, 36, 37, 59, 63, 80] [88, 29, 92, 52, 76, 66]
6
>>> next(sorter)
loop invariant maintenance: [19, 29, 36, 37, 59, 63, 80] [88, 92, 52, 76, 66]
7
>>> next(sorter)
loop invariant maintenance: [19, 29, 36, 37, 59, 63, 80, 88] [92, 52, 76, 66]
8
>>> next(sorter)
loop invariant maintenance: [19, 29, 36, 37, 52, 59, 63, 80, 88] [92, 76, 66]
9
>>> next(sorter)
loop invariant maintenance: [19, 29, 36, 37, 52, 59, 63, 76, 80, 88] [92, 66]
10
>>> next(sorter)
loop invariant maintenance: [19, 29, 36, 37, 52, 59, 63, 66, 76, 80, 88] [92]
11
>>> next(sorter)
Traceback (most recent call last):
File "<pyshell#26>", line 1, in <module>
next(sorter)
StopIteration
>>> print('we are done')
we are done
>>> nums
[19, 29, 36, 37, 52, 59, 63, 66, 76, 80, 88, 92]